Електротехнически материали

2 Теоретична обосновка

2.2 Относителна диелектрична проницаемост

   Разглежда се електрически кондензатор състоящ се от паралелни пластини с площ S (m²), намиращи се на разстояние d (m). Към пластините (електродите) на кондензатора се прилага електрическо напрежение U, и се разглеждат два случая:

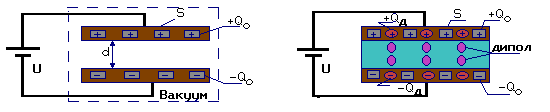
                                                                                                                                                                 а)                                                       б)

Фиг.2.

   На фиг.2.а е показан кондензатор поместен във вакуум. В този случай на неговите пластини възниква заряд Q_o.

   На фиг.2.б е показан показан кондензатор между пластините на който е поставен диелектрик с дебелина равна на разстоянието между пластините.

    При поляризацията на диелектрика в електрическото поле на срещуположните страни възникват заряди Q_Д, εзнакът на които е противоположен със знака на поляризационните заряди възникващи на повърхността на диелектрика. Следователно, пълния заряд на кондензатора с диелектрик ще бъде:   Q = Q_o +Q_д = ε_r.Q_o

където ε_r - относителна диелектрична проницаемост - един от важните параметри, характеризиращи диелектриците. Относителната диелектрична проницаемост представлява отношение на сумарният заряд на кондензатор с диелектрик, към заряда на същият кондензатор поместен във вакуум без диелектрик.

   От формулата се вижда, че когато Q_Д =0, което съответства на относителната диелектрична проницаемост на вакуума, то диелектричната проницаемост на всеки диелектрик ще бъде 1.

     При определянето на диелектричната проницаемост може да се използва капацитета на електрически кондензатор.

 От горната формула се вижда, че относителната диелектрична проницаемост на един диелектрик може да се даде като отношението на капацитета на кондензатор когато между електродите му е поставен диелектрик към отношението на капацитета на същият кондензатор поставен във вакуум, когато между елекродите му няма дилектрик.